Griechische Philosophie für Naturwissenschaftler: Die Pythagoreer.

freimaurer-wiki
aus spektrum.de, 10. Februar 2019

Die Vorsokratiker: Die Mathematik der Pythagoreer

Von Josef Honerkamp

Zu der Zeit, als Anaximenes in Milet die Tradition der ionischen Schule vertrat, wirkte in einem anderen Teil des griechischen Kulturkreises Pythagoras (ca. -570 bis -490).  Auf der Insel Samos geboren und aufgewachsen, soll er sich in seiner Jugend in Babylonien und Ägypten aufgehalten haben. Dort lernte er wohl die religiösen Anschauungen und auch das mathematische Wissen dieser Kulturen kennen. Um etwa -530 ließ er sich dann in Kroton nieder, einer durch Handel reich gewordenen Stadt in einer süditalieni- schen griechischen Siedlung und gründete dort eine Schule. Diese wurde zu einer verschworenen Gemein- schaft; er selbst wurde für seine Schüler eine unhinterfragte Autorität. Ein charismatischer Redner muss er auch gewesen sein, und er muss sie mit seinen Ideen, die er in Babylonien und Ägypten aufgenommen hat, stark beeindruckt haben. Mit dem Satz „Er hat es selbst gesagt“, soll bei den Pythagoreern manche Diskus- sion gar nicht erst aufgekommen sein (Schupp I, S.63). So sehen wir heute in dieser Schule starke religiöse Züge.

Vieles ist über Pythagoras geschrieben worden, vieles ihm zugeschrieben. Nichts davon gilt heute als gesichert. Es gibt keine Schriften von ihm, auch nicht von seinen Schülern, den Pythagoreern. Aus den antiken Quellen wie denen von Heraklit, Empedokles, Aristoteles und aus der Spätantike von Diogenes Laertios oder Jamblichos erfahren wir Widersprüchliches und höchst unterschiedliche Einschätzungen. 

Zwei Themen standen bei Pythagoras und seinen Schülern, den Pythagoreern, aber jedenfalls im Vorder- grund: Die Seelenwanderung und die Mathematik. Zu beiden Themen war Pythagoras vermutlich durch seine Reisen inspiriert worden. Auf die Vorstellungen, die sich die Pythagoreer von einer „Seele“ und einer „Seelenwanderung“ gemacht haben, will ich nicht eingehen. Die Pythagoreische Seelenlehre hat zwar eine große Wirkung entfaltet und spätere Philosophen wie insbesondere Platon stark beeinflusst. Sie war domi- nantes Thema des Neuplatonismus in den ersten nachchristlichen Jahrhunderten und ist über diese philo- sophische Strömung auch ins Christentum eingeflossen. Zum Erstarken des Logos im Denken der Men- schen hat diese Lehre aber nichts beigetragen.

Ganz anders verhielt es sich in dieser Beziehung aber mit dem Studium mathematischer Probleme. Eine Fülle von mathematischen Einsichten wurde gefunden. Ein ganz neues Feld für philosophische Über- legungen wurde entdeckt. Aristoteles berichtet in seinen Metamorphosen:

„In der gleichen Zeit, als jene Philosophen [Parmenides, Empedokles, Anaxagoras, Leukipp, Demokrit] tätig waren, aber auch schon vorher, fingen die als „Pythagoreer“ Bezeichneten an, mathematische Studien zu betreiben. Sie waren die ersten, welche diese Studien voranbrachten; und als sie darin erzogen worden waren, waren sie überzeugt, dass die konstitutiven Prinzipien des Mathematischen auch die konstitutiven Prinzipien der seienden Dinge seien.“ (Mansfeld & Primavesi, 2011, pp. 147, Nr.31).

Die Pythagoreer waren nach Aristoteles also die ersten, die das mathematische Wissen vermehrten, und Pythagoras hatte den Anstoß dazu gegeben. Dieses war der zweite große Anstoß in der Geistesgeschichte. Den ersten Anstoß hatten die ionischen Philosophen gegeben, als sie begannen, die Welt aus sich heraus zu erklären, nämlich mit Argumenten, die sich auf Regelmäßigkeit in der Natur stützten. Hier nun, im zweiten Schritt entdeckte man eine Sprache, in der man Regelmäßigkeiten notieren kann. Aber nicht nur dieses; man konnte in dieser Sprache auch Argumentationen liefern, die unabweisbar sind.

Und für das Verhältnis der „konstitutiven Prinzipien des Mathematischen“ zu den „konstitutiven Prinzipien der seienden Dinge“ haben die Pythagoreer nach Aristoteles eine erste Antwort geliefert. Wir werden im nächsten Blogbeitrag sehen, wie es ihnen damit ging. Später wird die Frage nach einem solchen Verhältnis noch sehr aktuell werden.

Aber schauen wir uns erst einmal die Studien an, welche die Pythagoreer und auch andere Philosophen, angesteckt durch diese, betrieben haben: 

Arithmetik

Mit dem Namen Pythagoras verbinden die Meisten den Satz von Pythagoras über die Beziehung zwischen den Quadraten der Seiten eines rechtwinkligen Dreiecks: Bezeichnet man die Katheten eines solchen Drei- ecks mit a und b, die Hypotenuse mit c, so gilt a² + b² = c². Diese Beziehung kannten schon die Babylonier und Ägypter und Pythagoras hatte wohl, wie übrigens Thales auch, solches Wissen von seinen Reisen mit- gebracht. Die Legende berichtet, dass Pythagoras bei Betrachtung einer ägyptischen Kachel zu einem Be- weis dieses Satzes angeregt worden war (Abb.1).

Abb. 1: links: Veranschaulichung des Satzes von Pythagoras, rechts: So könnte die Kachel (aber überall mit gleichen Strichen) ausgesehen haben, von welcher Pythagoras nach der Legende zu einem Beweis des Satzes inspiriert wurde. Die Quadrate über der Hypotenuse sind durch Strich-Punkte markiert. Die Quadrate über a, b, c enthalten zwei bzw. vier gleich große Dreiecke. (aus Honerkamp, 2018).

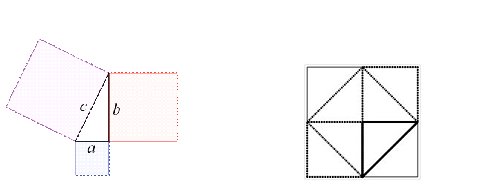
Hier haben wir es mit einer geometrischen Figur zu tun, aus der wir eine Aussage über die Beziehung dreier Zahlen, also eine arithmetische Relation, ableiten können. Das ist die wohl erste Verbindung von Geometrie und Arithmetik. Etwa 2.000 Jahre später sollte Descartes mit der „Analytischen Geometrie“ diese Verbindung noch so verstärken, dass fortan die Arithmetik zum Schwerpunkt der Mathematik wurde.

Die Griechen stellten ihre Zahlen damals noch durch Buchstaben dar, d.h. es gab prominente Zahlen, nämlich jene, welche wir heute 1, 2, …, 9, 10, 100,… nennen; jede andere Zahl wurde als Summe dieser Prominenten gesehen, und die Summanden wurden dann der Größe nach in Form von Buchstaben notiert. Wir kennen solch ein Additionssystem heute noch von den römischen Zahlen.

Im Rahmen einer solchen Zahlschrift ist das Rechnen sehr schwierig. Das mag Pythagoras dazu geführt haben, eine geometrische Zahlendarstellung zu erfinden, in der jede Zahl als eine Summe von Einsen gesehen wird. Für jede Eins wird ein Punkt notiert, wobei die Punkte dann zu einer bestimmten geome- trischen Figur angeordnet werden (Abb.2). So gibt es dann z.B. Quadratzahlen, Dreieckszahlen, Kubik- zahlen, usw.

 
Abb.2: Eine Quadratzahl (16=4²), Dreieckzahl (10 = 1+2+3+4) und eine Kubikzahl (8= 2³).

Aus solchen Figuren kann man dann schon viele weitere Beziehungen zwischen verschieden Zahlen ablesen, z.B. die Aussage, dass die Summe aufeinander folgender ungeraden Zahlen, wenn sie mit 1 beginnt, immer 
 eine Quadratzahl ist (Abb.3).

Abb. 3: Eine Folgerung aus Quadratzahlen (aus (Schupp, 2003a, p. 74))

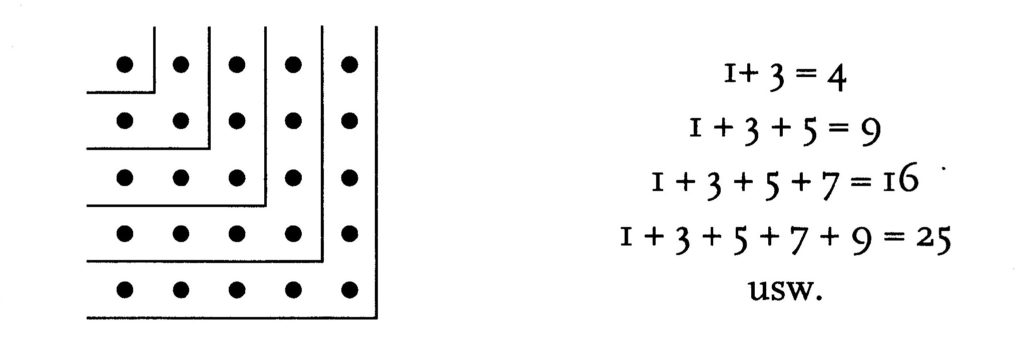
Wenn man noch auf der rechten Seite dieser Abbildung die letzte Zeile schreibt als:

(1 + 3 + 5 + 7) + 9 = 25, also 16 + 9 = 25, oder 4² + 3² = 5²,

erhält man ein so genanntes pythagoräisches Zahlentripel, d.h. drei Zahlen, bei der sich das Quadrat der größten als Summe der Quadrate der beiden kleineren Zahlen darstellen lässt. Auf diese Weise entdeckt man, wie einfach man solche Zahlentripel bilden kann:  Jede Summe solcher ungeraden Zahlen, die mit einer Quadratzahl endet, liefert ein Tripel. Man nehme also nur eine ungerade Quadratzahl, sagen wir 25 = 5², und bilde

1 + 3 + … + 23 + 25 = 169, also 144 + 25 = 169, oder 12² + 5² = 13².

Solche Zahlentripel kannten schon die Babylonier, und da man auf deren Keilschrifttafeln eine große Anzahl von solchen Tripeln fand, müssen Verfahren zur Bildung solcher Tripel schon viel länger bekannt gewesen sein.  Selbst in der Megalith-Kultur Südenglands soll man für Konstruktionen das Wissen um solche Tripel benutzt haben (van der Waerden, 1983, p. 9).

Inspiriert durch solche Erfahrungen entdeckten die Pythagoreer viele Beziehungen zwischen zwei, drei oder vier Zahlen, z.B. das arithmetische und das geometrische Mittel, auch das harmonische Mittel. Vermutlich kannten sie auch schon den „goldenen Schnitt“. Heute würde man solche Studien unter dem Titel „Zahlentheorie“ verbuchen.

Geometrie

Die Geometrie wurde bei allen diesen Studien über Verhältnisse von Zahlen nicht vernachlässigt. Besonders in Ägypten haben Thales und Pythagoras viel über Geometrie lernen können. Nach Nilüberschwemmungen mussten die Ägypter oft ihre Felder wieder rekonstruieren. Da war es sehr nützlich, wenn man wusste, wie man Rechtecke konstruieren konnte, und vor allen Dingen, wenn man den Flächeninhalt eines Feldes berechnen konnte.

Nicht nur rechte Winkel und Rechtecke waren wichtig. Auch Kreise, Dreiecke und andere Vielecke wollten konstruiert werden, in der Praxis – und bei den Griechen dann auch auf dem Papyrus mit Zirkel und Lineal, ganz ohne Hinblick auf einen Nutzen. Und man wollte die Flächeninhalte auch solcher Flächen berechnen können.

Ein notorisches Problem war bei den Babyloniern und Ägyptern die Berechnung des Flächeninhaltes F eines Kreises gewesen. Man wusste wohl, dass F proportional zum Quadrat des Radius sein muss, aber die Proportionalkonstante, die wir heute mit π bezeichnen, war nicht genau bestimmbar. Die Babylonier hatten den Wert 3 für diese Konstante benutzt, die Ägypter (16/9)² = 3,1604…, der Pythagoreer Antiphon der Sophist (5. Jhdt.v.Chr.) machte sich zunutze, dass man den Flächeninhalt von regelmäßigen Vielecken schon zu bestimmen wusste, näherte den Kreis durch solche Vielecke, und erhielt dadurch einen Näherungswert, der umso besser ist, je mehr Ecken dieses Vieleck hat. Diese Methode sollte Schule machen. Bryson von Herakleia (-450 bis -390) betrachtete nicht nur regelmäßige Vielecke, die in den Kreis einbeschrieben sind, sondern auch solche, die den Kreis umschreiben. Er erhielt somit zwei Näherungen, eine, die kleiner, eine andere, die größer als der gesuchte Wert ist. Archimedes sollte die Methode dann zu einer Perfektion treiben, die man heute nur bewundern kann  (Honerkamp, 2018, p. 82ff).

Nicht nur Flächen, sondern auch dreidimensionale Körper im Raum wurden studiert, neben der Kugel waren insbesondere die Vielflächner (Polyeder, nach ἔδρα gr. = Sitzplatz, καδ-έδρα gr. = Katheder) interessant. Diese sind Körper, die von mehreren regelmäßigen Flächen begrenzt sind. So gibt es einen Tetraeder (Vierflächner), der Würfel ist ein Hexaeder, es gibt einen Oktaeder (Achtflächner), einen Dodekaeder (Zwölfflächner) und einen Isokaeder (Zwanzigflächner) (siehe Abb.4).


 
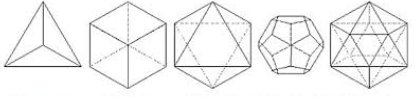
Abb.4: Die fünf platonischen Körper: Tetrader, Hexaeder, Oktaeder, Dodekaeder, Isokaeder.*
 
Wie der Mathematiker Theaitetos (-415 bis -369) zeigen konnte, besitzen alle diese einen bestimmten Punkt im Innern, der von allen Ecken gleich weit entfernt ist, sodass sich alle diese Vielflächner in einer Kugel einschreiben lassen. Er bewies auch, dass es keine weiteren Polyeder dieser Art geben kann. Die Regelmäßigkeit dieser Körper und ihre Einzigartigkeit hat Platon später veranlasst, Tetraeder, Hexaeder, Oktaeder und Isokaeder den Elementen Feuer, Erde, Luft und Wasser zuzuordnen, ganz im Sinne der Pythagoreer, die ja alles in der Natur von der Zahl beherrscht sehen. Platon hat diesen Körpern also einen mythischen Glanz gegeben; das führte dazu, dass man sie später „platonische Körper“ nannte.

Der französische Wissenschaftshistoriker André Pichot listet in seinem Werk Die Geburt der Wissenschaft einundzwanzig griechische Mathematiker des 6. und 5. Jahrhunderts v.Chr. auf (Pichot, 2000, p. 371ff). Viele mathematische Theoreme in Geometrie und Arithmetik sind von diesen gefunden worden. Auch Lehrbücher, „Elemente“ genannt, muss es in vorsokratischer Zeit gegeben haben, mit denen man Neulinge in die Mathematik einführen wollte. Keines davon ist uns überliefert worden. Erst aus der Zeit um -300 liegt uns ein solches Lehrbuch vor. Dafür ist es wohl das vollständigste und ausgereifteste Werk, aus dem wir den Stand der damaligen Mathematik entnehmen können. Es sind die „Elemente“ des Euklid von Alexandria. Dieses Werk besteht aus drei Kapiteln („Büchern“) über Arithmetik und 10 Kapiteln über Geometrie. Es hat einen kaum überbietbaren Einfluss in der Geistesgeschichte der westlichen Welt gehabt hat, vor allem, weil es die Geometrie in Form eines axiomatisch deduktiven Systems darstellen konnte und damit die logische Ordnung des dargestellten Wissens transparent machte. Ich werde zu entsprechender Zeit darauf zurückkommen.

Musik

Es gab noch ein anderes, sogar konkreteres Feld, auf dem die Pythagoreer entdeckten, dass sich Beziehungen im Raum auf Beziehungen zwischen Zahlen abbilden lassen. Dieses Feld war die Musik, die sie auf der Lyra spielten, und hier konnte man sogar mit den Sinnen Beziehungen zwischen Natur und Zahlen erfahren.

Das „Tetrachord“ besaß vier Saiten, denen man je nach Länge und Spannung durch Zupfen, Streichen oder Schlagen einen bestimmten Ton entlocken konnte. Wenn man zwei Saiten gleichzeitig zupfte, hörte man einen Klang, den man als harmonisch empfand, wenn die Längen der beiden Saiten in einem ganzzahligen Verhältnis wie 1:2, 2:3, 3:4 standen. Insbesondere bei dem Verhältnis 2:1 hörte sich der Klang fast wie ein einzelner Ton an. Betrachten wir hier die einfachste Form eines Tetrachords (s.a. Wikipedia: Tetrachord). 

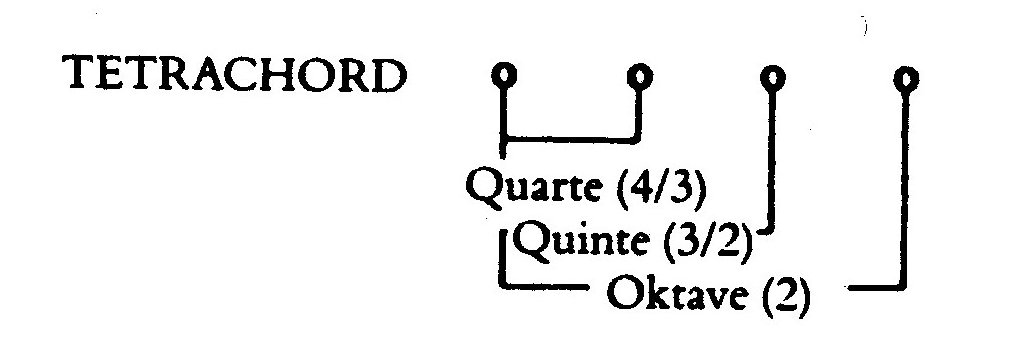Abb. 5:  Die Saiten eines Tetrachords und die Verhältnisse der Längen benachbarter Saiten (nach (Pichot, 2000)). Achtung: Hier werden die Töne von links nach rechts tiefer!

Sei die erste Saite ganz links die kürzeste. Die zweite, dritte und vierte Saite mögen dann 4/3, 3/2 bzw. 2/1 mal der Länge der ersten, sein. Wir nennen die Töne dann C’, G, F und C, die Frequenz der Töne G, F, C sind 3/4, 2/3 und 1/2 mal der Frequenz des Tons C’ der linken Saite. Der Pythagoreer Philolaos gibt den Intervallen bestimmte Namen, später hießen diese dann Quarte (von C’ nach G), Quinte (von C nach F) und Oktave (von C’ nach C) (Abb.5).

Abb.6: Die Saiten eines Oktochords und die Verhältnisse der Frequenzen benachbarter Saiten in der pythagoreischen Stimmung (nach Pichot,200, p.385)

 

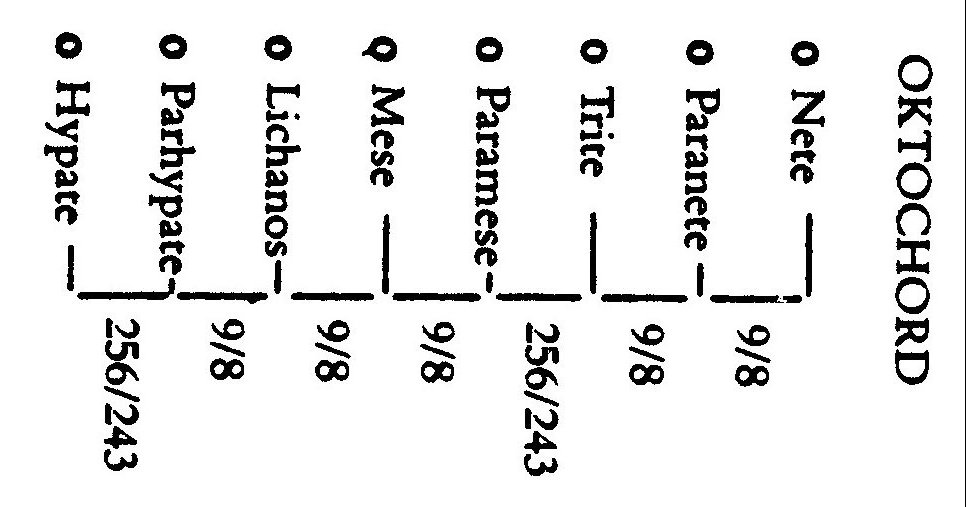
Für ein „Oktochord“ mit acht Saiten brauchte man eine feinere Unterteilung (Abb.6). So führte Philolaos zunächst eine „Sekunde“ als Abstand zwischen Quarte und Quinte ein (von G nach F, von Mese zu Paramese). Für diesen ergibt sich das Verhältnis der Frequenzen von (3/4):(2/3) = 9/8. Mit zwei auf einander folgenden Sekunden (Ganztönen) kann man vom tiefsten Ton C (Nete) ausgehend aber noch nicht den Ton F (Paramese) erreichen. Der verbleibende “Abstand” ist (4/3):(9/8)²= 256/243. Dieses Intervall nennt man einen „Halbton“, die Griechen nannten es Diёsis (von δί-ειμι, gr. =hindurchgehen).

Das Intervall von G nach C’, von der Mese zu der Hypate, ist auch eine Quarte und es ergibt sich ein gleiches Bild wie von C nach F.

Solch ein „Halbton“ ist also ein Intervall, bestehend aus zwei Tönen mit einem Frequenzverhältnis von 256/243. Es ist aber nicht wirklich so etwas wie die Hälfte des Intervalls eines Ganztons. Denn setzt man zwei solcher Intervalle auf einander, so ergibt sich ein Intervall mit dem Frequenzverhältnis von (256/243)², was nicht gleich 9/8 ist. Es fehlt noch ein ganz kleines Intervall mit Frequenzverhältnis

(9/8) : (256/243)² = 531441/524288.

Dieses Intervall nannte man heute das pythagoreische Komma (von gr. κόπτειν->κόμμα = so etwas wie “Abschnitt”, siehe Duden, Herkunftswörterbuch). Man müsste den „Halbton“ also genauer einen kleinen Halbton nennen, und es gibt dann auch einen großen Halbton, ein Intervall, das um das pythagoreische Komma größer ist. 

Solange man auf dem Oktochord spielt, und alle, die gleichzeitig spielen, den gleichen Grundton C benutzen, spielt dieses pythagoreische Komma keine Rolle. 

Diese Bestimmung eines Vorrates von sechs Tönen zwischen den zwei Tönen einer Oktav bei gegebenem Grundton führt zur so genannten Pythagoreischen Stimmung. Sie wird also bei einem solchen Oktochord verwirklicht.

Die sechs Töne (nun von “unten” beginnend: D, E, F, G, A, H) kann man auch so bestimmen: Von einem gegebenen Ton aus finde man jeweils die reine Quinte (Frequenzverhältnis 3/2). Ergibt sich dabei ein Ton oberhalb des betrachteten Intervalls, setze man den Ton eine Oktave tiefer, halbiere also die Frequenz. Geht man also von C aus, so erhält man nach und nach: G, D‘->D, A, E‘->E, H. Jetzt fehlt noch das F. Dann sollte man doch von F an beginnen, erhält also nun: F, C, G, D, A, E, H.

Will man nun den Vorrat an Tönen vergrößern, so kann man dafür weiterhin die Quintenregel nutzen, erhält also Töne, die wir Fis, Cis, Gis, Dis, Ais nennen könnten, weil deren Frequenzen jeweils um eine Diёsis höher als F, C, … sind. Der nächste Ton wäre dann Eis, und das müsste wieder F sein. Das stimmt aber nicht, denn zwischen H und dem Fis dieser Konstruktion liegen zwei kleine Halbtöne (H-C und E-F), statt nur eine wie bei den anderen solchen Intervallen. Das Intervall H-Fis ist also eine zu kleine, keine reine Quinte, eine „Wolfsquinte“ (weil sie „heult wie ein Wolf“). Man muss also, wenn man die Regel strikt befolgen will, die Frequenz des Fis noch um das Pythagoreische Komma erhöhen und damit alle folgenden Töne auch. Die Frequenz des dann schließlich erreichten Eis wäre also um dieses Komma höher als F. Das zeigt sich auch, wenn man diese Konstruktion rechnerisch nachvollzieht. Es ist

(3/2)¹²: 2⁷ = 531441/524288.

Würde man von F „abwärts“ im gleichen Maße die Töne B, Es, As konstruieren, erhielte man die Quintenzirkel in der üblichen Form. Dann zeigt sich bei den Tönen Gis/As, dass sich der „Zirkel“ nicht ganz schließt. Der Ton Gis ist um das Pythagoreische Komma höher als das As.

Das Pythagoräische Stimmungssystem war bis ins 16.Jahrhundert in Mode. Nach langem Experimentieren hat man im 16./17. Jhdt. die gleichstufige Stimmung kennen gelernt. In dieser ist die Oktave in zwölf Intervalle gleicher Frequenzverhältnisse f aufgeteilt. ES muss also f¹² = 2 sein, damit ist f = 1,05946…. > 1,05349… = (256/243). 

*) Zu dem Punkt ist mir an anderer Stelle ein Schnitzer unterlaufen. Das ist peinlich, hat den Gedankengang aber nicht beeinträchtigt. JE